kb0nly
Full Access Member
(Maybe Sticky This)
Getting ready to change the fluid and filter in my 03' and i came across the problem of determining which transmission i actually have, since 03' seems to be the dividing line for the Liberty in this respect.
In the process i found the gaskets, filters, and everything needed for both transmissions and i wanted to share this info in case anyone else needs it.
First off, the number of bolts on the pan.
42RLE = 13 Bolts
45RFE = 15 Bolts
There is a gasket available for the 42RLE, despite popular belief that it must be done with RTV. There is actually two types available, a fiber gasket and a cork gasket. The one pictured is the cork.
As opposed to the 45RFE the 42RLE only has one filter and only one style of that filter for both 2x4 and 4x4 applications.
Here is the 45RFE pan gasket, there is a rubberized and a plain cork gasket available, this is the black rubberized version.
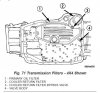
Now for the filters. First of all it would appear both the 2x4 and 4x4 applications of this transmission need this filter.
Then depending on what you have, 2x4 or 4x4, there is a different sump filter for it.
Here is the 2x4 filter front and back.
Here is the 4x4 filter front and back.
Getting ready to change the fluid and filter in my 03' and i came across the problem of determining which transmission i actually have, since 03' seems to be the dividing line for the Liberty in this respect.
In the process i found the gaskets, filters, and everything needed for both transmissions and i wanted to share this info in case anyone else needs it.
First off, the number of bolts on the pan.
42RLE = 13 Bolts
45RFE = 15 Bolts
There is a gasket available for the 42RLE, despite popular belief that it must be done with RTV. There is actually two types available, a fiber gasket and a cork gasket. The one pictured is the cork.
You must be registered for see images
As opposed to the 45RFE the 42RLE only has one filter and only one style of that filter for both 2x4 and 4x4 applications.
You must be registered for see images
Here is the 45RFE pan gasket, there is a rubberized and a plain cork gasket available, this is the black rubberized version.
You must be registered for see images
Now for the filters. First of all it would appear both the 2x4 and 4x4 applications of this transmission need this filter.
You must be registered for see images
Then depending on what you have, 2x4 or 4x4, there is a different sump filter for it.
Here is the 2x4 filter front and back.
You must be registered for see images
You must be registered for see images
Here is the 4x4 filter front and back.
You must be registered for see images
You must be registered for see images
Last edited by a moderator: